嘉师论坛 | 学科专家与嘉定青年教师的云端对话（十八）：结构化教学的实践与思考

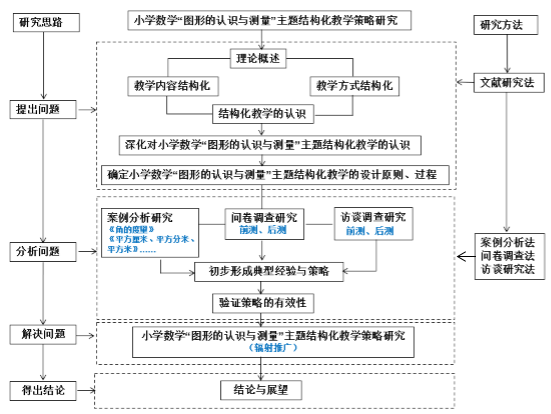
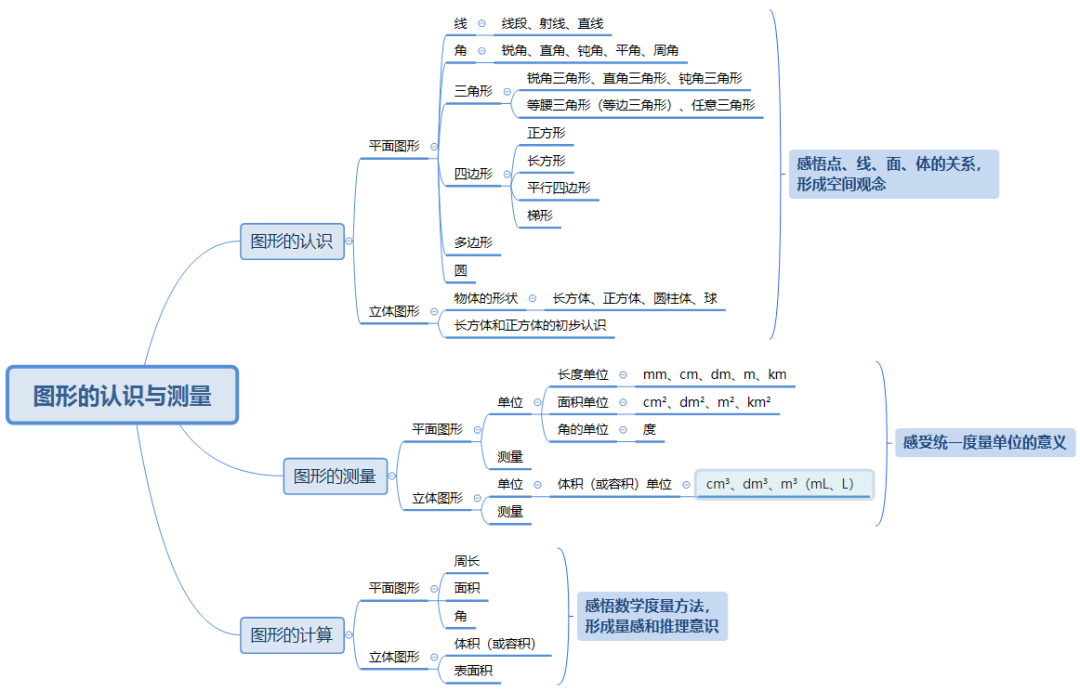
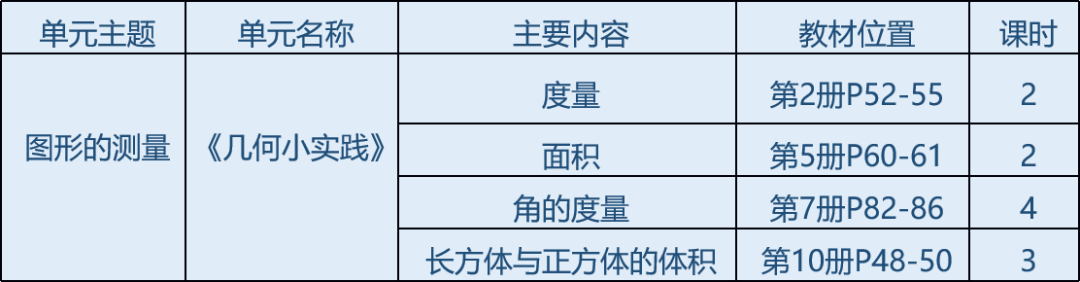
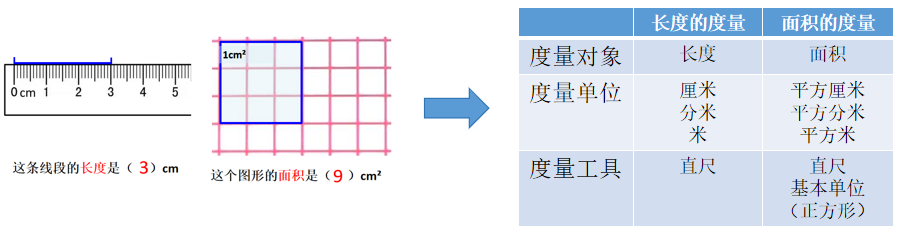
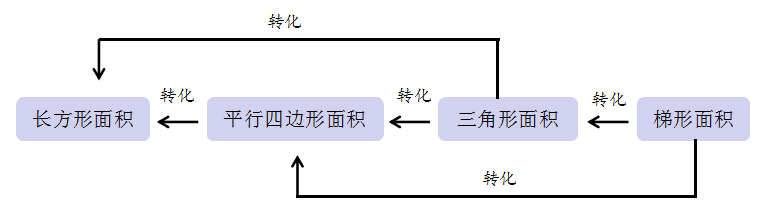
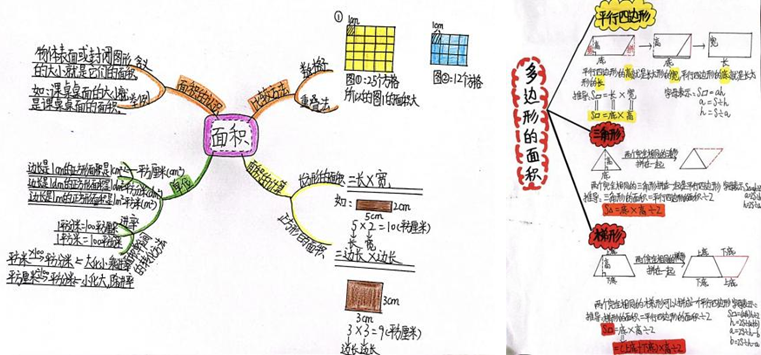
上海市嘉定区普通小学  吕 昊

一、问题的缘起

《义务教育数学课程标准（2022年版）》明确指出核心素养导向下课程内容组织的重点是对内容进行结构化整合。然而，在教学实践中，部分教师对于结构化教学存在着理解上的偏差或缺乏相应的实施策略等问题。

我通过教师调查问卷发现教师是有实施结构化教学意识的，但是教师通过把握知识间的本质、建立知识间的联系，整合教材内容，进行结构化教学的能力还不够；通过学生访谈，发现学生在学习中建立知识结构的能力较薄弱，对学习方法迁移性的感悟不强，不善于找到知识与方法之间核心互化的关联并将新知转化为旧知。此次调查，无疑给我在接下来把握结构化教学策略研究的方向上起到了投石问路的作用。我结合参加上海市小学数学中青年教学评比《角的度量②》一课中关于结构化教学的思考，选取沪教版小学数学“图形与几何”领域的“图形的认识与测量”主题为例，进行教材内容的知识结构分析，并深入课堂实践研究，探索结构化教学策略，培养学生的结构化学习意识和能力，帮助学生形成结构化思维，发展学生数学核心素养。

二、对结构化教学认识的深化

结构化教学强调在教学时要整体思考教学内容，并形成教学方式上的一致性，因此需要从教学内容和教学方式两方面来思考。    

数学教学内容的呈现是“点”状的，而知识之间是相互联系的。结构化教学需注重知识的内在联系，以知识的内在联系去系统的理解知识和把握知识，促使学生将知识结构内化为认知结构，建构数学整体的知识框架。

“图形的认识与测量”主题的教学内容包括立体图形和平面图形的认识，线段长度的测量和角的度量，以及图形的周长、面积、体积（或容积）和角的大小的计算。通过横向梳理知识间的内在联系，将具有共同特征的知识内容进行整体建构，凸显知识间的内在联系；纵向梳理学段间的知识结构，突破固定单元的限制，实现学段间的知识融合，形成“图形的认识与测量”主题知识结构图。

虽然“图形的认识与测量”主题的教学内容分散在小学数学教材的不同单元中，但所采取的教学方式应该一致，即从一节课到一类课。对于相同、相近的学习内容，教师需要把握正确的教学方式，关注数学学科的基本原理、概念及其之间的联系，形成对所学知识的整体把握，发展学生的结构化思维。

 “图形的测量”均以“数+度量单位”的形式呈现度量结果，表示含有度量单位的个数。因此，我以“度量单位的累加”为统领，抓住“度量”的本质，整合这一大单元内容，让学生经历充分的自主探究、类比迁移，形成这一大单元的学习经验，逐步感悟到长度的度量、面积的度量、角的度量、体积的度量本质的一致性。

三、对结构化教学策略的探索

我在开展结构化教学实践中注重知识内容、学习方法、学习过程的连续性，并通过优化教学设计，深入课堂实践研究，探索出了以下结构化教学策略。

数学的结构化教学就是要学生掌握数学中的定理、公式、数学思想及它们之间的关系、本质，引导学生发现共同点，实现数学学习的类比迁移。学生一旦学会类比迁移的方法，就能将一个问题的解决方法类比迁移到一类问题的解决中，找到问题的核心，最终感悟知识本质的一致性。

转化的本质是将未知、陌生、复杂的问题转化为已知、熟悉、简单的问题，最终使原始问题得到解决。在教学中，教师要引导学生关注“图形的认识”“图形的测量”它们内在的关联性，并从关联中找到互相转化的途径，从解决问题的思想方法上统领，促进学生的思维结构化。

教师可以在每一个单元的末尾或其他合适的时机中，组织学生对一个板块的知识内容进行总结梳理，根据自己的理解，将所学的知识结构用思维导图、知识树、逻辑图、表格等工具可视化呈现，经历数学知识再抽象、分类、归纳的过程，完善原有思维结构。

在教学过程中，教师要整合教学内容，积极开展主题活动，促进学生融会贯通，加强感悟知识间的内在关联，以此促进数学思维的结构化。

四、我的思考

数学知识不是孤立的，它们有着密切的联系。在实施结构化教学的过程中，教师需要看清知识的“前世今生”，厘清知识的“结”，在课堂上运用策略有的放矢，让学生拔“结”生长，自主建“构”，最终形成结构化思维，培育核心素养。在后续教学实践中，教师要进一步思考如何去激活学生内隐的经验，让学生运用内隐经验自主优化完善认知结构。